Computer Science 210
Data Structures
Fall 2017, Siena College
This week's lab will give you lots more practice with recursive methods. You will be assigned a partner for this lab. Only one submission per group is needed.
Getting Set Up
You will receive an email with the link to follow to set up your GitHub repository recursion-lab-yourgitname for this Lab. One member of the group should follow the link to set up the repository on GitHub, then that person should email the instructor with the other group members' GitHub usernames so they can be granted access. This will allow all members of the group to clone the repository and commit and push changes to the origin on GitHub. At least one group member should make a clone of the repository to begin work.
Please answer lab questions in the README.md file in your group's GitHub repository.
Remember, no work will be graded unless the names of all group members are in each file.
Tracing Recursive Methods
public void f(int n) {
System.out.println(n);
if (n > 1) {
f(n - 1);
}
}
public void g(int n) {
if (n > 1) {
g(n - 1);
}
System.out.println(n);
}
public void h(int n) {
System.out.println(n);
if (n > 1) {
h(n - 1);
}
System.out.println(n);
}
Iteration vs. Recursion
For this part of the lab, you will be writing a series of Java applications similar in structure to the Powers example. As in that example, you will need to create a keyboard Scanner to read in a number from the terminal and use System.out.println to issue a prompt and report your answer.
These programs will be graded as practice programs.
Factorials
The first problem we are going to solve is that of computing factorials. From math, you know that the factorial of a positive integer n, denoted n!, is the product of all the numbers from 1 up to n.
First, write a main method in the Factorial class that prompts for and reads in a positive integer. You need not worry about error checking the input for this assignment. (2 points)
Next, write an iterative method loopFactorial that takes a single int as its parameter and returns the factorial of that value. Recall that an iterative method uses loop structures like for and while loops to do its work. Also update your main method to call the loopFactorial method on the number entered by the user, and print out the value returned. (6 points)
Finally, write a recursive method recFactorial that uses that formulation to compute factorials. Also update your main method to call the recFactorial method on the number entered by the user, and print out the value returned. You should leave in the call to loopFactorial so you can see that the answers are consistent. (9 points)
Sum of Squares
The next problem we are going to solve is that of computing the sum of the first n squares.
First, write a main method in the SumSquares class that prompts for and reads in a positive integer. You need not worry about error checking the input for this assignment. (2 points)
Next, write an iterative method loopSumSquares that takes a single int as its parameter and returns the sum of the squares up to that value. Also update your main method to call the loopSumSquares method on the number entered by the user, and print out the value returned. (6 points)
Finally, write a recursive method recSumSquares that uses that formulation to compute the sum of squares. Also update your main method to call the recSumSquares method on the number entered by the user, and print out the value returned. You should leave in the call to loopSumSquares so you can see that the answers are consistent. (9 points)
n Choose k
Now, we will consider the function Choose(n,k), which is the
number of different ways you can choose k items from among n
items. For example, if you have three items {a,b,c}, there are
3 ways to choose 2 of them: {a,b}, {b,c}, and
{a,c}. So Choose(3,2) = 3.
This is a case where recursive thinking leads to an elegant solution. We can define Choose(n,k) recursively as follows: Choose(n,0) is 1 for all n >= 0, and Choose(0,k) is 0 for all k >= 1. For all n > 0 and k > 0, Choose(n,k) is equal to the number of ways you can choose k-1 items from among n-1 items added to the number of ways you can choose k items from among n-1 items.
First, write a main method in the Choose class that prompts for and reads in two positive integers that will be used as n and k. You need not worry about error checking the input for this assignment. (2 points)
Next, write a recursive method recNChooseK that uses that formulation to compute the value of Choose(n,k). Update your main method to call the recNChooseK method on the numbers entered by the user, and print out the value returned. (9 points)
Recursive Printing and Drawing
In the class RecursivePractice, you will find three methods to be completed. Rather that writing a main method that calls these, we will test them by running them directly in BlueJ. You will be shown/reminded how to do this during lab. These methods will be graded as practice programs.
Complete the recursive method printIt so that it prints n
asterisks, followed by the same number of exclamation points. For
example, printIt(5) would print "*****!!!!!". Use
recursion. Use no loops or local variables. The base case is
provided. (6 points)
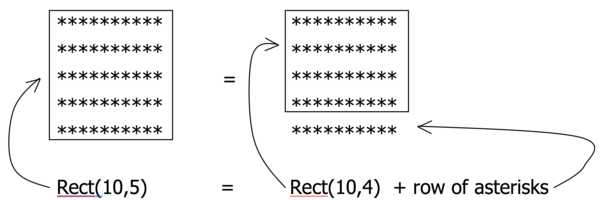
Next, consider the rectangle of asterisks below. It has width 10 and height 5. You could define this rectangle recursively as a rectangle of width 10 and height 4 followed by a row of 10 asterisks. A height 0 rectangle is the base case, in which case nothing is printed.

Complete the drawRectangle method, which recursively draws a rectangle of width w and height h. (6 points)
Finally, consider the right triangle of asterisks below. It has a base of length 6. Think about how you could define this triangle recursively.
*
**
***
****
*****
******
Complete the method drawRightTriangle which recursively draws a triangle of base length b. The second argument is the number of spaces that appear before the base of the triangle. For example, for the base 6 triangle above there are 0 spaces before the base, so you would invoke the method with b = 6 and leadingSpaces = 0. But if you remove the bottom row from this triangle, you are left with a triangle of base length 5 with 1 leading space before the base. (8 points)
Submitting
Your submission requires that all required deliverables are committed and pushed to the master for your repository's origin on GitHub. That's it! If you see everything you intend to submit when you visit your repository's page on GitHub, you're set.
Grading
This assignment is worth 100 points, which are distributed as follows:
| > Feature | Value | Score |
| Trace f | 4 | |
| Trace g | 4 | |
| Trace h | 4 | |
| Question 2: n! values | 2 | |
| Factorial input | 2 | |
| loopFactorial method and call | 6 | |
| Question 3: n! recursive mathematical formulation | 5 | |
| recFactorial method and call | 9 | |
| Question 4: sum of squares values | 2 | |
| SumSquares input | 2 | |
| loopSumSquares method and call | 6 | |
| Question 5: sum of squares recursive mathematical formulation | 4 | |
| recSumSquares method and call | 9 | |
| Question 6: Choose(n,k) values | 5 | |
| Question 7: Choose(n,k) recursive mathematical formulation | 5 | |
| Choose input | 2 | |
| recNChooseK method and call | 9 | |
| printIt method | 6 | |
| drawRectangle method | 6 | |
| drawRightTriangle method | 8 | |
| Total | 100 | |