Nearly any topic in a course working with data will be more interesting for students if the data has connections to the real world and if they can visualize the data and results in a meaningful way. When using graph data, such as in a data structures or algorithms class, it needs to be small enough to be manageable, but large enough to be interesting. This might consist of a small road system, airline flight schedules, or even the layout of a campus or building. The Map-based Educational Tools for Algorithm Learning (METAL) project provides data and visualization capabilities for this purpose. METAL's graph data sets range in size from a few vertices and edges to several hundred thousand. Its data is derived from the Travel Mapping (TM) Project, and represents highway systems from around the world. METAL's interactive code-level algorithm visualization capabilities with debugger-like controls are intended to aid student understanding of graph and other algorithms. Students can also implement graph algorithms themselves in a programming language of their choice and display, in map form, the results of computations using those algorithms when applied to METAL data.

Project news and discussions can be found in the METAL section of the Travel Mapping Forum.

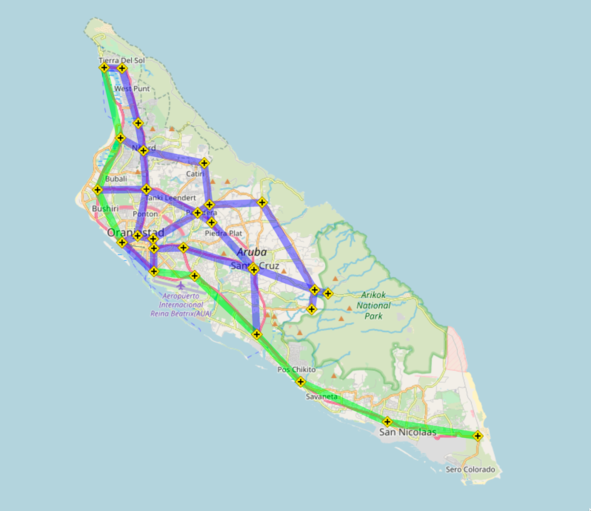
Wouldn't it be more fun, interesting and engaging to work with this graph than this one? (which I used for several years)

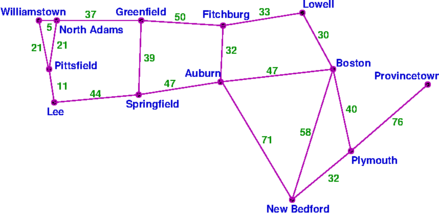
TM's data is updated daily, and an updated collection of graphs is generated almost as frequently from this data. Stable archives of graph data are saved periodically. These graphs represent the highways in various regions, countries, and highway systems, and are provided in well-defined formats. Those interested can read more about where it comes from and how it is generated. The highway systems and regions in Travel Mapping (TM), from which METAL derives its data, vary in size, meaning graph data comes at a variety of scales. They vary in size from just a handful of vertices and edges for systems in small island nations to several hundred thousand for the global data set.

The Highway Data Examiner (HDX) is is a browser-based tool which uses Leaflet to provide map capabilities. HDX supports plotting of the TM and derived data, and a suite of interactive algorithm visualizations.

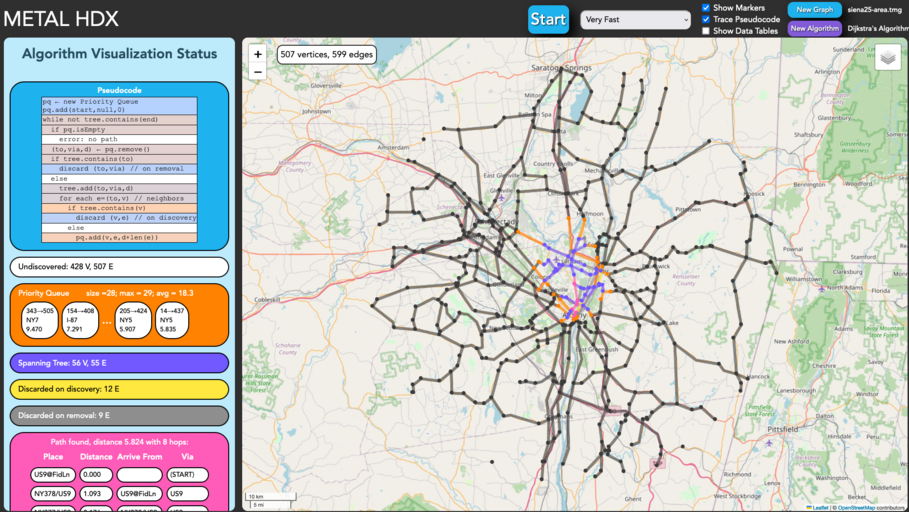
METAL's most engaging feature is its interactive algorithm visualizations. After loading a graph data file into HDX, an algorithm can be chosen, along with any needed parameters (e.g., a starting vertex for a traversal). A set of controls are used to start, pause, reset, or change the speed of the simulation. During the simulation, the data plus the contents of key variables and data structures are displayed in map and, optionally, tabular form. The algorithm's code can be simulated line-by-line, and conditional breakpoints can be used to stop the simulation at points of interest. Our expanding set of algorithms supported include simple vertex- and edge-based searches, closest pairs, graph traversals, finding connected components, finding convex hulls, quadtree construction, space-filling curve traversals, a recursive coordinate bisection partitioner, Dijkstra's algorithm and the A* algorithm for single-source shortest paths, Prim's algorithm and Kruskal's algorithm for minimum spanning trees, brute-force and an approximation of the traveling salesperson algorithm, bridge detection, and graph coloring.

METAL's graph data files can be used as input for class examples or assignments in a data structures, algorithms, or other courses. This data was first used in a laboratory assignment for a data structures course at Mount Holyoke College where students were required to build a graph structure representing a highway system then perform Dijkstra's algorithm to compute the shortest route between two specified waypoints. Student programs generated output files listing the road segments along the shortest path. These were then uploaded to a course web server, where an instructor-provided program (an early predecessor to today's HDX) used the Google Maps API to visualize their results. Students were able to develop and debug their programs using small data sets like the Hawaii Interstates, then use those programs to compute much more complex routes using the larger data sets. The software has been updated and extended and used in numerous courses at Siena College and The College of Saint Rose. Successful assignments include the creation of custom classes to store the information about the points and connections between them, storing these points and connection in a data structure and then searching within and sorting those points (a great way to motivate comparators), finding convex hulls, performing graph traversals, and more advanced graph algorithms including Dijkstra's algorithm.

Recent efforts have included the development of easily-adoptable learning modules that use METAL data and algorithm visualization capabilities.