Computer Science 507
Software Engineering
Spring 2014, The College of Saint Rose
For this week's lab, we will refine our techniques for unit testing a bit. Unit testing techniques might include equivalence testing, state-based testing, boundary testing, domain testing, and control flow-based testing (statement, branch).
You may work alone or in groups of up to size 4 for these exercises.
Equivalence Partitioning
Equivalence partitioning is a blackbox testing technique that minimizes the number of test cases. Possible inputs are partitioned into equivalence testing classes, and a test case is selected from each class. We make the assumption that the system behaves in a similar way for all members of an equivalence class.
For example, suppose we have a function or method that compute the number of days in a month. Since we cannot reasonably test all possible month/year combinations, we find equivalence classes of inputs and sample inputs and outputs for each to perform what are hoped to be fairly complete tests. In this example, we will want combinations of months with different numbers of days, covering both leap years and non leap years.
One possible set of equivalance classes for this might be:
We will not write actual unit tests for such a method, but hopefully you see how you could.
Now consider the Triangle program on mogul.strose.edu in /home/cs507/s14/labs/testing.
Control Flow Adequacy Testing
We now consider a whitebox testing mechanism. Note that a method or program can be represented by a flow graph.
A segment is represented by a node (circle) in the flow graph. A segment is one or more contiguous statements with no conditionally executed statements. That is, if we start executing a segment, there is no way to proceed except through the entire segment.
A conditional transfer of control is a branch. A branch is represented by an outgoing edge in the flow graph.
The entry point of a method is represented by the entry node, which is a node no incoming edges. The exit point of a method is represented by the exit node, which has no outbound edges.
For example, the method:
public int fun1(int x){
k = 0;
while (x <= 10 && k < 3){
if (x%2 != 0)
k = k + 1;
x = x + 1;
}
if (x < 0){
x = 10;
k = 0;
}
return k;
}
would be represented by the flow graph:
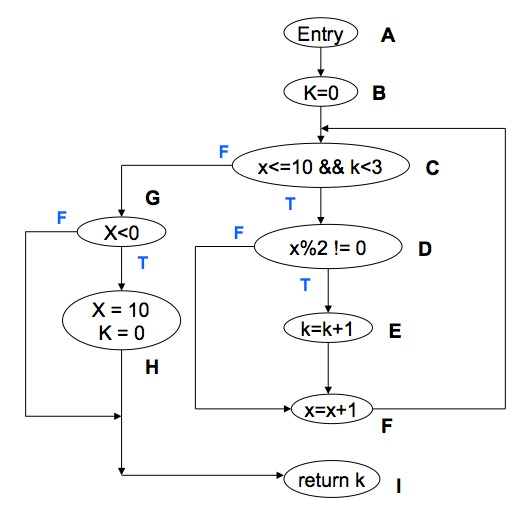
where each segment is labelled with a letter.
Given such a flow graph, we would like to form tests that exercise all parts of the flow graph.
The first standard is statement coverage. A set P of execution paths satisfies the statement coverage criterion iff for all nodes n in the flow graph, there is at least one path p in P s.t. n is on the path p. We would like to generate test inputs that will cause each statement in the program to execute at least once.
A second standard is branch coverage. A set P of execution paths satisfies the branch coverage criterion iff for all edges e in the flow graph, there is at least one path p in P s.t. p contains edge e. Here, we want to generate test inputs to exercise both the true and false outcomes of each decision.
A larger example:
public int fun2(int x, int y){
k = 0;
while (x <= 10 && k < 10){
if (x%2 != 0){
k = k + y;
k = k - 2;
}
x = x + 1;
k = x + k;
}
if (x < 0){
x = y;
k = k + x;
}
return k;
}
Submission
Before 6:00 PM, Monday, March 24, 2014, submit your lab for grading. Package up all required files into an appropriate archive format (.tar.gz, .zip, and .7z are acceptable) and upload a copy of the using Submission Box under assignment "Testing".
Grading
This lab will be graded out of 30 points.