We were discussing memory management in paged systems.
Much like what we did to compare CPU scheduling algorithms, we will evaluate page replacement algorithms by running them on a particular string of memory references (reference string) and computing the number of page faults on that string. The string indicates the logical pages that contain successive memory accesses. We count the number of page faults needed to process the string using the given algorithm.
In all our examples, the reference string is 1, 2, 3, 4, 1, 2, 5, 1, 2, 3, 4, 5.
We know that there must be a minimum of 5 page faults here, as 5 different pages are referenced. If we have 5 frames available, that is all we'll ever have. So we consider cases where we have 3 or 4 frames available, just to make it (slightly) interesting.
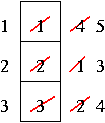
First-In-First-Out (FIFO) Algorithm
You guessed it - the first page in is the first page out when it comes time to kick someone out.
If we have 3 frames available:

This produces a total of 9 page faults. Let's add a frame.
4 frames:
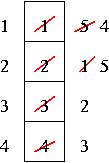
We got 10 page faults! This is very counterintuituve. We would expect that adding available memory would make page faults occur less frequently, not more. Usually, that is the case, but we have here an example of Belady's Anomaly. Here, adding an extra frame caused more page faults.
FIFO replacement is nice and simple - we know our victim immediately. However, it may produce a large number of page faults given an unfortunate reference string.
Optimal Algorithm (OPT)
We can't do better than replacing the page that will not be used for longest period of time in the future, so let's consider that.
4 frames example:
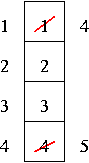
6 page faults.
Problem: we can't predict the future, at least not very accurately.
So it's not practical, but it is useful to see the best we can do as a baseline for comparison of other algorithms.
Least Recently Used (LRU) Algorithm
Select the frame that we have not used for the longest time in the past.
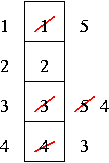
8 page faults. So we did better than FIFO here, but it's not optimal.
This one can actually be used in practice.
It can be implemented directly by maintaining a timestamp that gets updated each time a frame is accessed. Then when a replacement decision is needed, the one with the the oldest time stamp is selected.
This is expensive in terms of having to update these timestamps on every reference, and involves a linear search when a victim is being selected.
A stack-like implementation can eliminate the search. When a page is references, it moves to the top of the stack. A doubly-linked list can be used to make this possible:
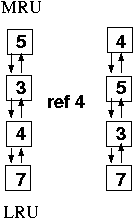
This requires 6 pointer updates each time a page is referenced that was not the most recently used. This is still expensive, and would require hardware support to be used in practice.
LRU Approximation Algorithms
LRU is a desirable algorithm to use, but it is expensive to implement directly. It is often approximated.
If we have one reference bit available, we can do a second-chance or clock replacement algorithm.
Here, we treat our collection of frames as a circular list. Each has a reference bit, initially set to 0. It is set to 1 any time the page is referenced. There is also a pointer into this list (the hand of a clock, hence the name) that points to the next candidate frame for a page replacement.
When a page replacement is needed, the frame pointed to is considered as a candidate. If its reference bit is 0, it is selected. If its bit is 1, the bit is set to 0, and the pointer is incremented to examine the next frame. This continues until a frame is found with a reference bit of 0. This may require that all frames be examined, bringing us around to the one we started with. In practice, this is unlikely.
It is called a second chance algorithm, as after a frame has had its reference bit set to 0, it has a second chance - if it is referenced before the pointer makes its way back around again, it will not be removed. Thus, frequently-used pages are unlikely to become victims.
Second-chance/clock does not do well with our running example.
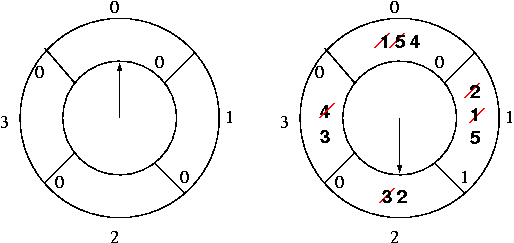
10 page faults! We ran into the same unfortunate victim selection that we saw with FIFO with 4 frames. We need a larger example to see the benefit.
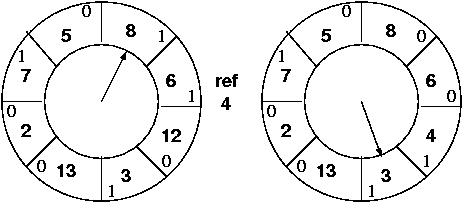
Pages 8 and 6 get their second chance, and may be referenced before the clock makes its way around again.
An enhancement to the clock algorithm called Gold's Clock Algorithm uses a second bit - a "dirty" bit in addition to the reference bit. The dirty bit keeps track of whether the page had been modified. Pages that had been modified are more expensive to swap out than ones that have not, so this one gives modified pages a better chance to stick around. This is a worthy goal, though it does add some complexity.
Counting Algorithms
One more group of algorithms to consider are those that keep track of the number of references that have been made to each page.
It is not clear which approach is better. LFU would need to be combined with some sort of aging to make sure a page that is used a lot early on, getting a big count, can still leave eventually when its usage stops.
Implementations of these suffer from the same problems that the direct LRU approaches do. They're either too expensive because of needed hardware support or too expensive because of the searching needed to determine the MFU or LFU page.
Allocation of Frames
So far, we have considered how to assign pages of a process' logical memory to a fixed set of allocated frames (local replacement). We also need to decide how many frames to allocate to each process. It is also possible to select the victim from a frame currently allocated to another process (global replacement).
Each process needs a certain minimum number of pages.
Allocation may be fixed:
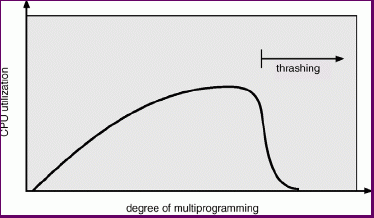
Thrashing
Thrashing occurs when a process does not have "enough" frames allocated to store the pages it uses repeatedly, the page fault rate will be very high.
Since thrashing leads to low CPU utilization (all processes are in I/O wait frequently having page faults serviced), the operating system's medium or long term scheduler may step in, detect this and increase the degree of multiprogramming.
With another process in the system, there are fewer frames to go around, and the problem most likely just gets worse.
Paging works because of locality of reference - a process access clusters of memory for a while before moving on to the next cluster. For reasonable performance, a process needs enough frames to store its current locality.
Thrashing occurs when the combined localities of all processes exceed the capacity of memory.
We want to determine the size of a process' locality to determine how many frames it should be allocated. To do this, we compute the set of logical pages the process has referenced "recently". This is called the working set of the process.
We define "recently" as a given number of page references in the process' history. This number is called the working set window is usually denoted Delta.
The working set will vary over time.
The appropriate selection of Delta allows us to approximate the working set size, WSSi, of process Pi. If Delta is too small, WSSi will not encompass the entire locality. If Delta is too large, pages will remain in the locality too long. As Delta increases, WSSi grows to encompass the entire program.
The total demand for frames in the system is D = SigmaWSSi.
Thrashing by at least one process is likely when D > m, where m is the number of frames. If the system detects that D > m, then it may be appropriate to suspend one or more processes.
For the reference string is 1, 2, 3, 4, 1, 2, 5, 1, 2, 3, 4, 5, with Delta= 4, the working set grows to {1,2,3,4} by time 4, but note that at time 8, it contains {1,2,5}.
A bigger and better example is coming as part of the next homework.
Tracking the working set exactly for a given Delta is expensive and requires hardware support to hold the time stamps of the most recent access to each page. See the text for details of how to do this.
Windows NT and Solaris both use variations on the working set model.
Program Structure
We have stated that programs exhibit locality of reference, even if the programmer made no real effort to encourage it. But program structure can affect performance of a paging scheme (as well as the effectiveness of other levels of the memory hierarchy).
Consider a program that operates on a two-dimensional array:
int A[][] = new int[1024][1024]
and the system has a page size of 4KB. This means 1024 ints fit in one page, or one page for each row of our matrix A.
Program 1:
for (j=0; j<1024; j++)
for (i=0; i<1024; i++)
A[i][j] = 0;
Program 2:
for (i=0; j<1024; j++)
for (j=0; i<1024; i++)
A[i][j] = 0;
Assume a fixed allocation of 10 frames for this process. Program 1 generates 1024 × 1024 page faults, while Program 2 only generates 1024.