October 26, 2000

Computer Science 338 Midterm Exam Possible Answers

1. True/false statements. Easy points (2 points each). Justify each answer with a sentence or two.

a. One way to avoid deadlock in the Dining Philosophers problem is to introduce asymmetry.

True. Having some philosophers reach left first and some reach right first can break the deadlock.

b. Multiple reader processes can be allowed concurrent access to the shared database in the Readers-Writers Problem.

True. Only writers need exclusive access.

c. Communication with message passing and with shared variables are functionally equivalent.

True. Each can be simulated using the other.

d. The Unix system call fork() results in two processes which share all context.

False. The new process gets its own context.

e. An implementation of semaphores can avoid busy waiting when a process is blocked only if appropriate operating system support is provided.

True. Even with hardware support such as an atomic test and set, some busy waiting is still needed unless the OS can block a process.

f. On a distributed memory machine, a tree-structured barrier if often more efficient than a barrier implemented using a shared counter.

True. Shared memory access can be expensive in a distributed memory environment. It amounts to a series of messages, and in that case, the tree barrier will be more efficient.

g. After a call to pthread_create(), the new thread created always has the same process ID (as returned by getpid()) as the original thread.

False. It depends on the implementation of pthreads. Sometimes a thread is a process with its own PID, other times, it is a true thread within the same process.

h. The bakery algorithm we studied in class requires operating system support such as semaphores to achieve a solution to the critical section problem for n processes.

False. The availability of semaphores makes the bakery algorithm unneccessary.

2. Consider the following program, which uses the pthreads library. (15 points)

#include <stdio.h>
#include <unistd.h>
#include <string.h>
#include <pthread.h>

int global;

void print_word(void *arg) {
  char *message=(char *)arg;

  printf("%s\n", message);
  global=strlen(message);  // Note: strlen returns length of character string
  pthread_exit(0);
}

int main(int argc, char *argv[]) {
  pthread_t thr[3];

  printf("What's up doc?\n");
  pthread_create(&(thr[0]), NULL, (void *)&print_word, (void *)"Be vewy quiet,");
  pthread_create(&(thr[1]), NULL, (void *)&print_word, (void *)"I'm hunting wabbits,");
  pthread_create(&(thr[2]), NULL, (void *)&print_word, (void *)"Heh Heh Heh Heh");
  pthread_join(thr[2],NULL);
  pthread_join(thr[1],NULL);
  pthread_join(thr[0],NULL);
  printf("global=%d\n",global);
  return 0;
}

a. What might the output be when the program is run? Assume the pthread_create() calls are successful. (5 points)

What's up doc?
Be vewy quiet,
I'm hunting wabbits,
Heh Heh Heh Heh
global=15

b. Which lines of the output could print in a different order? What are the possible printed values of the variable global? (5 points)

The three lines printed by the threads can be in any order, or possibly even interspersed. The value of global could be 14, 15,or 20, depending on which thread sets it last.

c. When the parent thread (call it main) and the three child threads (call these child1, child2, and child3) are all executing concurrently, list all variables in existence and specify which threads have access to each variable. (5 points)

global is visible to main and to all three child threads. thr[3] is visible only to main. A copy of message exists within each child thread, and each is visible only to the thread in which is exists.

3. Concurrency is fun. (18 points)

Consider the following program:

int x = 2, y = 3;
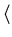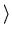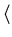co $\langle$ x = x + y; $\rangle$ // $\langle$ y = x * y; 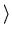$\rangle$ oc
print ("x=", x, ", y=", y);

a. What are the possible final values printed for x and y? (4 points)

x=5, y=15
x=8, y=6

b. Suppose the angle brackets are removed and each assignment statement is now implemented by three atomic actions: read a variable, add or multiply, and write to a variable. Now what are the possible final values printed for x and y? (6 points)

In addition to the above answers, a case arises where both processes read x and y before anyone has modified them, which leads to x=5, y=6.

c. Now consider the following program:

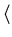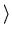
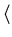co $\langle$ await (x >= 3) x = x - 3; $\rangle$
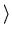
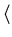// $\langle$ await (x >= 2) x = x - 2; $\rangle$
// $\langle$ await (x == 1) x = x + 5;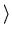 $\rangle$
oc

For what initial values of x does the program always, sometimes, or never terminate, assuming scheduling is weakly fair? What are the corresponding final values? Explain your answer. (8 points)

Call the statements S1, S2, and S3, from top to bottom.

If x<=0, nothing can happen, so it never terminates.

If x=1, S3 is followed by S1 and S2 in either order. This always terminates with x=1.

If x=2, S2 can run, but nothing else can. This never terminates.

If x=3, S1 or S2 can go. If S1 goes first, we're stuck. If S2 goes first, then S3 and then S1 can run, and we terminate with x=3. So this sometimes terminates.

If x=4, S1 or S2 can go. If S1 goes first, then S3 and then S2 can go and we terminate with x=4. If S2 goes first, we are stuck. So this sometimes terminates.

If x=5, S1 and S2 can run in either order, but S3 can never run. This never terminates.

If x=6, S1 and S2 can run in either order, followed by S3. This always terminates with x=6.

If x>6, S1 and S2 can run in either order, but S3 can never run. This never temrinates.

4. Atomicity and mutual exclusion (15 points)

a. What statments need to be atomic for the following matrix addition algorithm to be correct? (5 points)

  const int n=100;
  int A[n], B[n], C[n];
  /* compute A, B */
  co (i=0; i<n; i++) {
    C[i]=A[i]+B[i];
  }

None. Each concurrent statement operates on an independent part of the arrays.

b. Show pseudocode to implement mutual exclusion for two processes using an atomic Swap instruction, defined as follows: (10 points)

void Swap(bool x, bool y): 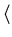$\langle$
bool temp;


temp = x; 

x = y; 

y = temp; $\rangle$

Shared data:

bool lock = true;

Process i:

while (1) {
  key = false;
  while (!key) swap(lock, key); // busy wait
  /* critical section */
  lock=true;
  /* noncritical section */
}

5. Message Passing (16 points)

a. Suppose a message passing library uses a reduction tree to compute the sum of the values of a distributed array. The array value on each process is in a variable val and contains that process' rank. The result is stored only on process 0. Show the data flow and intermediate operations that might be used by the message passing library to compute the sum for a reduction across 8 processes. (8 points)

Rank:  0  1  2  3  4  5  6  7
------------------------------
val:   0  1  2  3  4  5  6  7
       | /   | /   | /   | /
       +     +     +     +
       1     5     9     13
       |    /      |    /
       |   /       |   /
       |  /        |  /
       | /         | /
       +           +
       6           22
       |          /
       |        /
       |      /
       |    /
       |  /
       |/
       +
       28

d. Name two advantages and two disadvantages of using non-blocking (or asynchronous) sends and receives over blocking (or synchronous) sends and receives in a message passing application. (8 points)

Advantage: Can overlap computation with communication.

Advantage: Easier to avoid deadlock.

Disadvantage: Extra data structures and programmer responsibility for wait statements to ensure communication completion.

Disadvantage: Cannot immediately reuse send buffers.

Disadvantage: Cannot immediately use receive buffers.

6. The Roller Coaster Problem (20 points). Suppose there are n passenger processes and one car process. The passengers repeatedly wait to take rides in the car, which can hold C passengers, C < n. However, the car can go around the tracks only when it is full. Develop pseudocode for the actions of the passenger processes and the car process. Use semaphores for synchronization. You may assume the semaphores are fair.

Hints: The car process can be in one of two states: (i) waiting for passengers or (ii) going around the tracks. A passenger process can be in one of two states: (i) waiting for a seat in the car, or (ii) in the car (which could mean either waiting for more passengers to fill the car, or going around the tracks - your solution does not need to differentiate between these).

Shared data: semaphore avail_seat=C, ride_end=0, seats_taken=0;

Each of the n passenger processes:

while (1) {
  wait(avail_seat);  // wait in line
  signal(seats_taken); // claim a seat and sit in it
  // now sitting in car waiting for ride to complete
  wait(ride_end);  // wait for car to signal the end of the ride
}

The car process:

int counter;  // local variable - no mutex needed
while (1) {
  for (counter=0; counter<C; counter++) {
    wait(seats_taken);  // wait for each seat to be filled by a passenger
  }
  // go around the tracks
  for (counter=0; counter<C; counter++) {
    signal(ride_end);  // tell this riding passenger that they can leave
    signal(avail_seat);  // signal waiting passengers that a seat is open
                         // for the next trip around the tracks
  }
}

The final signal(avail_seat) in the car could be done by each passenger as he gets out of the car. Other solutions are possible.