Computer Science 210
Data Structures

Fall 2018, Siena College

Home     Syllabus     Schedule     Examples     Style Guide

In this lab, you will learn more about implementing methods of trees, in particular, binary search trees that store double values.

You will be assigned a partner to work with on this lab. Only one submission per group is needed.

As you finish each step, please have your instructor initial the hard copy of this lab handout you were issued to indicate successful completion.

Names:

GitHub userid used to accept the repository:

Learning goals:

1. To understand an existing implementation of a binary search tree.
2. To gain experience writing recursive methods on a binary search tree.
3. To gain experience writing iterative methods on a binary search tree.
4. To write a complex binary search tree method.

Submitting

As you complete each programming task, commit with a meaningful commit message and push to your group's GitHub repository for this lab.

Once all written items are initialed to indicate completion, turn in the hard copy of this lab handout you were issued.

Getting Set Up

You will receive an email with the link to follow to set up your GitHub repository for this Lab (trees-lab-yourgitname). One member of the group should follow the link to set up the repository on GitHub. Other group members will receive a subsequent email with a link to follow that will grant them the rights to clone the repository and commit and push changes to the origin on GitHub.

The BST Implementation and Test Code

To start, study the implementation of the BinarySearchTree class and take a look at the main method in Test.java.

Warmup Recursive Tree Methods

You will be adding recursive implementations of methods in BinarySearchTree to compute and return the sum of all values in the BST:

  public double sum();

and to compute the number of leaf nodes in the BST:

  public int numLeaves();

Now it's time to implement them. In each case, you will need to write a recursive helper method. Also add code to test each in the main method of Test.java. You will need to build a couple more BSTs to test all important cases.

More Recursive Tree Methods

Add recursive implementations of methods in BinarySearchTree to do each of the following.

A contains method, which returns true if value v is in the tree and false otherwise. (6 points)

public boolean contains(double v);

A method numAs, which returns a count of the number of values in the tree whose value is in the "A" grade range, i.e., 90-100. (6 points)

public int numAs();

A method getSmallest, which returns the smallest data value in the tree. To keep things simple, assume there is always at least one value in the tree, so that a smallest value exists. (5 points)

public double getSmallest();

While you are not being required to write out base cases and recursive cases for these, be sure you understand and can describe those in English before attempting to write your implementations.

As with the warmup recursive methods, each of these will require a recursive helper method. Also add code to test each in the main method of Test.java (3 points).

Note: to be accepted, your implementations should only search the parts of the tree where the values being sought might be found. Take advantage of the fact that you are dealing with a BST!

Some Iterative Tree Methods

Now, let's write some BST methods without recursion. Documentation is provided for what each of these should do in BinarySearchTree.java and tests are provided in the main method of TestBinarySearchTree.java.

  public void addIterative(double value);
  public double getLargestIterative();
  public void removeLargestIterative();

Removing Arbitrary Values from a BST

We conclude by implementing a more complicated BST method: removing a single instance (note that there could be more than one in the tree) of an arbitrary value from the BST.

  public void remove(double value);

You will implement this method iteratively, and we will do it in a two steps: 1) finding the node that contains the value, and then 2) writing the code to remove it. There are several cases to consider, so the lab will step you through each part of the implementation. 27 required test cases plus 5 bonus test cases are included in the main method of TestBinarySearchTree.

To remove a value, you first must be able to find the Node containing the value to be removed. Do this now in the remove method by using the provided variables current and parentOfCurrent, each of which is of type Node. Start by initializing current to the root and parentOfCurrent to null. Then use a loop to move current down the tree until it either reaches a Node containing the value or becomes null (meaning the value is not in the tree). The variable parentOfCurrent needs to follow current down the tree, always one node behind it (since our BST structure does not maintain parent references in its nodes). The variable parentOfCurrent will be necessary when removing the value in step 2.

Now, we remove the Node containing the value. To remove the Node, there are 4 cases to deal with. Implement and test each case (using the main method in TestBinarySearchTree).

Case 1

The current node is null, indicating the value was not found in the tree. In this case, the method just returns with no further work. This case is already implemented for you! (But you also get no further credit for completing it...)

Case 2

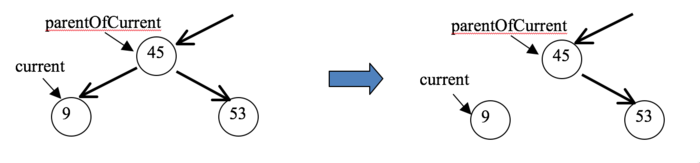
The current node has no children. In this case, change the link of parentOfCurrent that refers to current to null. This is illustrated below when removing the value 9 from the tree. Run the test program and make sure you get full points for this case before going on to the next case.

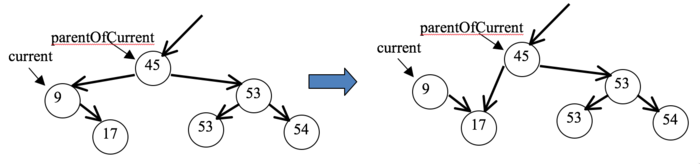
Case 3

The current node has only one child. For example, we might be removing 9 from the tree on the left below.

In this situation, change the parentOfCurrent's child link and make it point to the only child of 9, as shown on the right above. Observe that node 9 is no longer part of the tree (because you can't get to it from the root). Java's garbage collection will eventually reclaim its memory.

Note that in this example, current was to the left of parentOfCurrent so we changed parentOfCurrent's left child link. But if current had been on the right of parentOfCurrent, we would have changed parentOfCurrent's right child link instead. So you'll have to test for this and change the correct link.

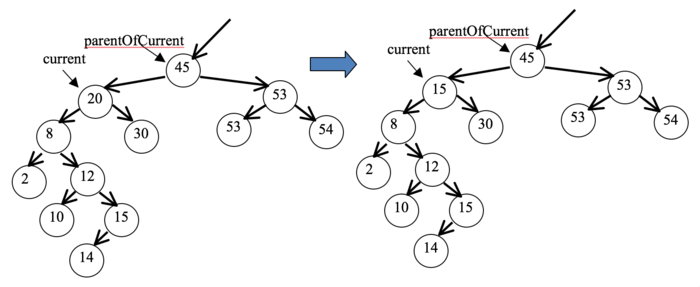
Case 4

In the last case, current has two children. You can take care of this case in two substeps. First, find the largest element in current's left subtree and copy its data into the current node, overwriting the target value and thus removing it. For example, consider removing 20 from the tree below on the left. The largest value in 20's left subtree is 15, so 15 replaces the 20 at the current node, as shown on the right.

You can get the largest in current's left subtree using the method getLargestIterative(Node n) that you already wrote.

Copying the 15 into the current node eliminates the 20, but now we have an extra copy of 15, one of which we must eliminate. It is easy to remove the 15 in current's left subtree, because it is the largest value in that subtree and you have the method removeLargestIterative(Node n) that you wrote earlier in the lab!

There are 5 bonus points available in the main method of TestBinarySearchTree that are to support removal of the root of the tree. No need to worry about those until everything else is working.

Don't forget to commit and push all of your code for this lab to your group's GitHub repository.