Computer Science 210
Data Structures

Fall 2018, Siena College

Home     Syllabus     Schedule     Examples     Style Guide

In this week's lab, we will practice more with recursion, and experiment with searching and sorting. There is a lot more thinking and planning here than actual coding.

You will be assigned a partner on this lab. Only one submission per group is needed.

As you finish each step, please have your instructor initial the hard copy of this lab handout you were issued to indicate successful completion.

Names:

Learning goals:

1. To practice writing recursive methods that operate on arrays.
2. To trace more interesting recursive methods with recursive call trees.
3. To introduce Java's Comparable interface and the required compareTo method for implementing classes.
4. To study the execution of the selection sort and insertion sort algorithms.

Submitting

As you complete each programming task, commit with a meaningful commit message and push to your group's GitHub repository for this lab.

Once all written items are initialed to indicate completion, turn in the hard copy of this lab handout you were issued.

Getting Set Up

You will receive an email with the link to follow to set up your GitHub repository for this Lab (searchingsorting-lab-yourgitname). One member of the group should follow the link to set up the repository on GitHub, then that person should email the instructor with the other group members' GitHub usernames so they can be granted access. This will allow all members of the group to clone the repository and commit and push changes to the origin on GitHub.

Recursion on Arrays

For your first task, you will be filling in a few methods in RecursivePractice.java. You may test by writing a main method or by calling the methods within BlueJ and providing appropriate parameters.

No loops!

The first method is to find the minimum value in the array among the values in a given range of indices.

For your implementation, break the subrange down into a slightly smaller version of the problem, solve it, then use that answer and what you know about the part of the array you didn't include in the subproblem to get an answer to the whole thing.

Now, write the body of the recursive minimum method.

For the next method, you are going to write a recursive method to count how many times your lucky number (which you'll provide as a parameter) occurs in a given array among the values in a given range of indices.

This time, instead of breaking a problem of size n into a problem of size n-1 and using the solution to that and the n^th item to form a solution, we are going to break the problem into two equal sized (or as close as we can get) parts, and using those solutions to get a solution to the original problem.

Now, implement your recursive countlucky method.

For the third array-based recursive method, you will write a method negative that checks if the array contains any negative values anywhere among the values in a given range of indices.

Before we think about the recursive formulation and implementation, let's look at an iterative solution.

  public static boolean negative(int a[], int first, int last) {

     boolean foundNegative = false;
     for (int i = first; i <= last; i++) {
         if (a[i] < 0) foundNegative = true;
     }
     return foundNegative;
  }

Hopefully you have already spotted the inefficiency here. Once foundNegative is set to true, it can never become false again, so why bother continuing the search? If a[first] was negative, we have our answer in a single comparison!

Thinking in terms of reducing our problem of size n to a problem of size n-1, let's formulate a recursive approach.

Now complete your recursive negatives method.

Recursive Call Trees

Next, we will study a few recursive methods using a recursive call diagram, which you will see gives a level of detail somewhere between our recursive call diagrams from last week and the complete memory diagrams from earlier in the semester.

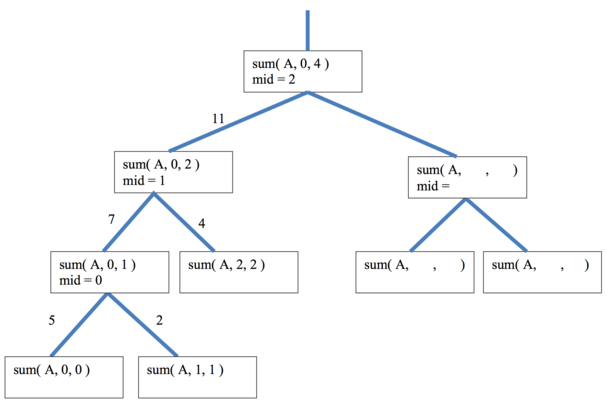
Consider the recursive method below for summing the values in an array from position first to last, inclusive. Below the method is the recursive call tree showing all the recursive calls made when the method is initially invoked with the array a containing values {5, 2, 4, 1, 6} and first = 0 and last = 4. The lines show the recursive calls made, and the number next to the line shows the value returned by the call.

public static int sum(int[] a, int first, int last) {
    if (first == last) {
        return a[first];
    }
    else {
        int mid = (first + last) / 2;
        int left = sum(a, first, mid);
        int right = sum(a, mid+1, last);
        return left + right;
    }
}

public static void mystery(String s, int d) {
    if (d == 0) {
        System.out.print(s + " ");
    }
    else {
        mystery(s + "0", d - 1);
        mystery(s + "1", d - 1);
    }
}

Making Ratios Comparable

For the next part of the lab assignment, you will be seeing how we can create our own Comparable objects that could be used with generic code like the search methods in the BinSearch example. Both Ratio.java and BinSearch.java are in your repository. Put the names of all group members working on this task in those files now. Yes, do it now. Now. Really. Don't make me ask you again.

Your first modification is to have the Ratio class implement the Comparable interface. So the class header would become:

public class Ratio implements Comparable<Ratio>

This tells Java that this class can be treated as a "comparable" object like Integer, Double, String, and many others.

The message is telling you that you just told Java that Ratio objects are "comparable" but didn't tell Java how to do that comparison. We do it in the same way that we compare other objects: by providing a compareTo method.

Write a compareTo method in the Ratio class. It will need to have a method header like this:

    public int compareTo(Ratio other)

For now, have your method simply return 0 in all cases. You should now be able to compile Ratio.java again.

Next, we need to make the compareTo method work properly.

Your only experience so far with compareTo methods is probably the one built in to the String class. Recall that for String references s1 and s2, the call

s1.compareTo(s2)

will return 0 if s1.equals(s2); a value less than 0 if this s1 is lexicographically less than s2; and a value greater than 0 if s1 is lexicographically greater than s2.

For Ratio objects, we want to do the same thing: if we have two Ratio objects r1 and r2, the call

r1.compareTo(r2)

should return 0 if r1.equals(r2) (keep in mind this means that the 1/2 should be equal to 3/6); a value less than 0 if this r1 is less than r2; and a value greater than 0 if r1 is greater than r2.

It doesn't matter what positive or negative value you return, as long as it's positive when it should be, negative when it should be, and 0 when they're equal.

Complete the compareTo method for the Ratio class and write a short main method in your modified Ratio class to test your new compareTo method. Be sure all three possible return values are tested.

Now, add code to the main method of BinSearch that creates an array of several Ratio objects and peforms a variety of successful and unsuccessful searches. Be sure to test all important cases.

Notice that you didn't need to write a new method that knows about Ratio objects! By teaching your Ratio objects how to compare themselves to other Ratios, they can now be used with the generic binary search that works on any Comparable objects. This is pretty excellent.

Sorting

Read the topic notes about selection sort and insertion sort and look at the recursive implementations of those algorithms in the SortingComparisons example. You may do these last two diagrams on the back of a page in this packet or on a separate sheet.

Don't forget to commit and push all of your code for this lab to your group's GitHub repository.